26个字母全排列,求第k项

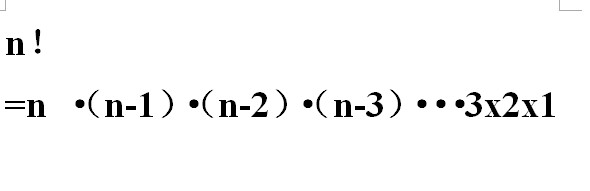
思路

如果有4个字母abcd全排列，求第13项

第13项/3! = 2.....余1
因此，第0个字母是abcd中的第2项，即c
此时剩下abd

余数1/2! = 0.....余1
因此，第1个字母是abd中的第0项，即a
此时剩下bd

余数1/1! = 1.....余0
因此，第2个字母是bd中的第1项，即d
此时剩下b

余数0/0! = 0
因此，第3个字母是b中的第0项，即b

最终结果是 cadb

根据上面的思路，写成如下js代码↓

4个字母全排列代码

//阶乘
function factorial(n,p=1) {
  if (n <= 1) {
    return p
  }
  var s = n * p
  return factorial(n - 1, s)
}


//获取第k项
function getResult(k) {
  if(k<0 || k>=factorial(4)){
    return 'k的值不在范围内'
  }
  
  var result = '';
  var j = 0;
  var letters = 'abcd';
  for (var i=3; i>=0; i--) {
    j = parseInt(k / factorial(i))  //商
    k = k % factorial(i)            //余数
    result += letters[j]
    letters = letters.replace(letters[j],'')
  }
  return result;
}

console.log( getResult(13) )

4个字母可以通过以上代码实现效果，但是26个字母不行。因为大整数超出范围会溢出，导致精度问题。
可通过BigInt解决！

BigInt解决精度问题

JS整数范围：
−9007199254740992 ~ 9007199254740992 （即正负2的53次方）
当超出该范围时，会存在精度问题，因此需要用到BigInt方法
关于BigInt的详细介绍：https://zhuanlan.zhihu.com/p/36330307

var x = 2**53;
var y = 2**53 + 1;
y-x // 竟然是0！！！

//下面，我们用BigInt来解决大整数的精度问题
var x = 2n**53n
var y = 2n**53n+1n
y-x // 1n
parseInt(y-x) // 1


//也可以用下面这种写法：
var x = BigInt(2**53)
var y = BigInt(2**53)+BigInt(1)
y-x // 1n
parseInt(y-x) // 1

26个字母全排列,求第k项

最终代码：

//阶乘
function factorial(n,p=1) {
  if (n <= 1) {
    return BigInt(p)
  }
  var s = BigInt(n) * BigInt(p)
  return factorial(n - 1, s)
}


function getResult(k) {
  if(k<0 || k>=factorial(26)){
    return 'k的值不在范围内'
  }
  
  var result = '';
  var j = 0;
  var letters = 'abcdefghijklmnopqrstuvwxyz';
  for (var i=25; i>=0; i--) {
    j = parseInt(BigInt(k) / factorial(i))
    k = BigInt(k) % factorial(i)
    result += letters[j]
    letters = letters.replace(letters[j],'')
  }
  return result;
}


console.log( getResult(0) ) //第0项：a~z

//最后一项
var lastItem = factorial(26) - 1n;
console.log( getResult(lastItem) ) //最后1项：z~a

【点击查看在线运行结果】